Afgevraagd.nl | De Inhoud en Oppervlakte van een Prisma
Voor het berekenen van de oppervlakte en inhoud van een prisma zijn een aantal dingen belangrijk. Zoals je waarschijnlijk al weet bestaat een prisma uit een veelhoek als boven- en grondvlak.
De formule voor de inhoud van een prisma is:
Inhoud Prisma = G · h
Waarbij G = Oppervlakte Grondvlak en h = hoogte van de prisma.
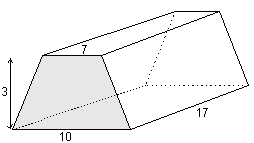
Nu moeten we eerst vaststellen wat het grondvlak is. Voor de meeste ruimtelijke figuren is dit het vlak waarmee het de grond raakt, maar voor een prisma is het grondvlak wat ingewikkelder. Meestal is dit grondvlak aangegeven (zoals hiernaast) maar soms is dat wat lastiger. Wat goed is om te onthouden is dat de grondvlakken in een prisma altijd identiek zijn!
De oppervlakte moet je berekenen door het optellen van alle losse vlakken. De meest gemaakte fout met deze vraag is dat je niet moet vergeten om alle vlakken op te tellen!
De oppervlakte van het grondvlak kunnen we berekenen. Het grondvlak is een trapezium en volgt dus de formule voor de oppervlakte van een trapezium:
Oppervlakte A = ½ · h · (a+b)
Waarbij h = hoogte van het trapezium, a = bovenste ribbe, b = onderste ribbe
In dit geval is de oppervlakte van het grondvlak dus:
Oppervlakte A = ½ · 3 · (7+10)
Oppervakte A = ½ · 3 · (17)
Oppervlakte A = ½ · 51
Oppervlakte A = 25,5
Vergeet de eenheid niet! (meestal cm2)
De inhoud van de prisma kunnen we nu ook invullen, omdat de hoogte gegeven is:
Inhoud prisma = 25,5 · h
Inhoud prisma = 25,5 · 17
Inhoud prisma = 433,5
Vergeet de eenheid niet! (meestal cm3)
Laten we nu ook nog even de rest van de oppervlakte berekenen. Hiervoor hebben we nog één onbekende nodig. Die berekenen we straks. Laten we een lijstje maken van alle vlakken:
Grondvlak = 25,5
Bovenvlak = 25,5
Lange zijde smal = 7 · 17 = 119
Lange zijde breed = 10 · 17 = 170
Nu hebben we nog twee vlakken nodig. Hiervoor hebben we nog één zijde nodig. Die moeten we even berekenen, en hiervoor knippen we het grondvlak even in 3:

Van deze figuur weten we dat de bovenste ribbe 7 is, en de gehele onderste ribbe is 10. We weten van de twee kleine driehoeken dus dat de kortste zijde dus 1,5 is. Ook weten we de hoogte: 3.
We zijn dus op zoek naar de schuine zijde.
Deze is te berekenen met de stelling van Pythagoras, en is gelijk aan √(3² + 1,5²) = √(9 + 2,25) = √(11,25)
De totale oppervlakte van de twee schuine vierhoeken is dus:
Oppervlakte = 2 · 17 · √(11,25)
Oppervlakte = 34 · √(11,25)
Oppervlakte = 114,04 (afgerond)
De totale oppervlakte is:
25,5 + 25,5 + 119 +170 +114,04 = 454,04. Afgerond is dit dus 454.
Vergeet de eenheid niet! (meestal cm2)
